Develog
15. 리스트 본문

1. 리스트 (List)

순서가 존재하는 데이터를 늘어놓은 형식의 자료구조.
구조가 단순한 리스트로 선형 리스트(Liner List) 또는 연결 리스트(Linked List)가 있다.
스택(Stack), 큐(Queue)도 리스트의 일종이다.
한 가지 주의할 점은, python의 리스트 자료형은 다른 언어의 리스트 자료형과 차이점이 있다는 것이다.
2. 연결 리스트 (Linked List)

여러 개의 노드(Node)가 주소를 참조하는 형식으로 연결되어 있는 구조의 리스트.
노드란, 연결 리스트를 이루는 각각의 원소(Elemet)들이다.
데이터와 뒤쪽 노드를 참조하는 포인터로 구성되어 있다.
노드의 종류로는 다음과 같다.
- 머리 노드 (Head Node): 연결 리스트 맨 앞의 노드
- 꼬리 노드 (Tail Node): 연결 리스트 맨 끝의 노드
- 앞쪽 노드 (Predecessor Node): 어떤 노드의 바로 앞 노드
- 뒤쪽 노드 (Successor Node): 어떤 노드의 바로 뒤 노드
3. 배열로 연결 리스트 구현하기
어떤 그룹의 회원 정보 데이터를 나타내는 튜플을 구성해보자.
(int형 회원번호, str형 이름, str형 전화번호)
data = [
(12, "John", "111-111-111"),
(33, "Paul", "222-222-222"),
(57, "Mike", "333-333-333"),
(69, "Rita", "444-444-444"),
(41, "Alan", "555-555-555"),
None,
None
]
3.1) 뒤쪽 노드 꺼내기
간단하게 인덱스 값을 1 증가시켜서 접근한 뒤, 값을 읽어오면 된다.
3.2) 노드 삽입 및 삭제
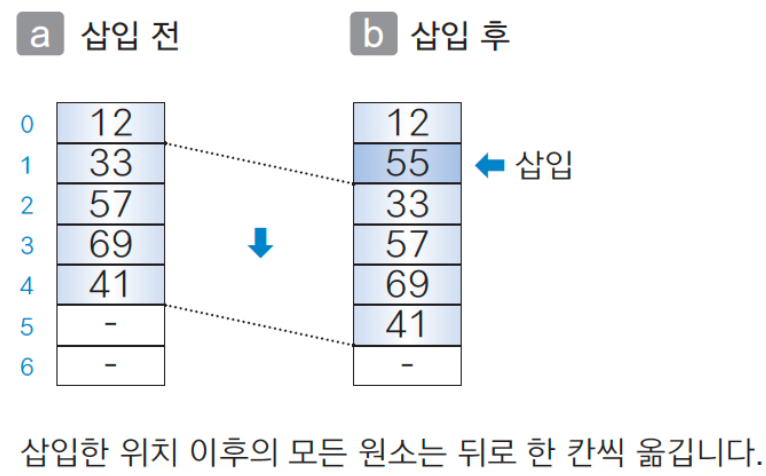
회원 번호가 55인 회원을 추가하려고 할 때, 추가한 원소 이후의 모든 원소가 1칸씩 뒤로 밀려야 한다.
삭제하는 경우에도 원소의 이동은 동일하게 필요하다.
데이터를 삭제/삽입하는 일이 많이 발생한다면, 배열을 사용한 구현은 매우 비효율적일 것이다.
4. 포인터로 연결 리스트 만들기
데이터를 삽입할 때 노드용 인스턴스를 생성하고, 데이터를 삭제할 때 노드용 인스턴스를 삭제한다.
연결 리스트는 배열과 달리 다음 노드의 메모리 주소를 참조하는 방식으로 구성되어 있기 때문에 배열처럼 단순한 연산으로 길이를 구할 수는 없다.
4.1) 빈 연결 리스트

연결 리스트가 비었을 경우, head 값은 None이 된다.
즉, head 노드가 꼬리 노드가 된다.
4.2) 노드가 1개인 연결 리스트

head가 참조하는 노드를 노드 A라고 가정하자.
노드 A는 머리 노드이자, 꼬리 노드이다.
노드 A의 next 필드 값이 None일 경우, 노드는 1개뿐이다.
(head가 참조하는 뒤쪽 포인터 값이 None)
4.3) 노드가 2개인 연결 리스트
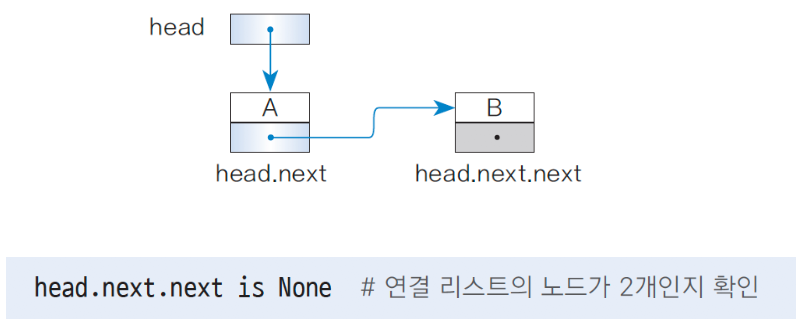
head가 머리 노드 A를 가리키며, 노드 A의 뒤쪽 포인터 next가 꼬리 노드 B를 가리킨다.
4.4) 꼬리 노드 여부 판단

Node형 변수 p가 리스트에 있는 노드를 참조할 때, p의 next 필드가 None이면 p는 꼬리 노드이다.
4.5) Node 클래스
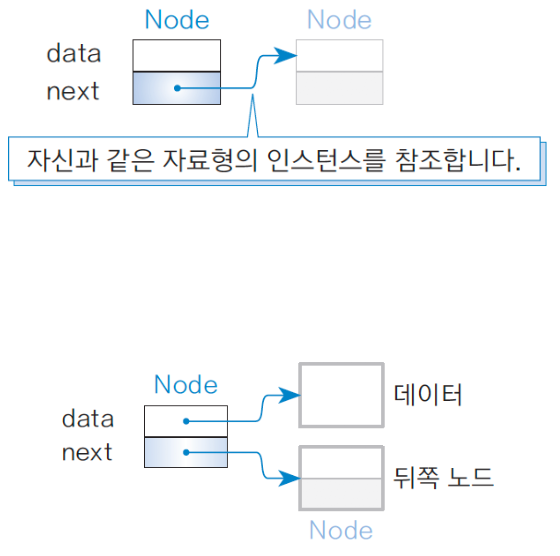
데이터용 필드 data와 별도로 자신과 같은 클래스형의 인스턴스 참조를 위한 필드 next로 구성된다.
- data 필드: 데이터 참조
- next 필드: 다음 노드 참조
노드는 자기 참조형 구조(Self-Referential Structure)를 이룬다.
(자신과 같은 형의 인스턴스를 참조하는 필드가 있는 구조)
from __future__ import annotations
from typing import Any, Type
class Node :
def __init__(self, data: Any = None, next: Node = None) :
self.data = data
self.next = next
4.6) LinkedList 클래스
연결 리스트를 구성하는 클래스이다.
class LinkedList :
def __init__(self) -> None :
self.no = 0
self.head = None
self.current = None
def __len__(self) -> int :
return self.no
def search(self, data: Any) -> int :
cnt = 0
ptr = self.head
while (ptr is not None) :
if (ptr.data == data) :
self.current = ptr
return cnt
cnt += 1
ptr = ptr.next
return -1
def __contains__(self, data: Any) -> bool :
return self.search(data) >= 0
def add_first(self, data: Any) -> None :
ptr = self.head
self.head = self.current = Node(data, ptr)
self.no += 1
def add_last(self, data: Any) -> None :
if (self.head is None) :
self.add_first(data)
else :
ptr = self.head
while (ptr.next is not None) :
ptr = ptr.nxt
ptr.next = self.current = Node(data, None)
self.no += 1
def remove_first(self) -> None :
if (self.head is not None) :
self.head = self.current = self.head.next
self.no -= 1
def remove_last(self) -> None :
if (self.head is not None) :
self.remove_first()
else :
ptr = self.head
while (ptr.next is not None) :
pre = ptr
ptr = ptr.next
pre.next = None
self.current = pre
self.no -= 1
def remove(self, p: None) -> None :
if (self.head is not None) :
if (p is self.head) :
self.remove_first()
else :
ptr = self.head
while (ptr.next is not p) :
ptr = ptr.next
if (ptr is None) :
return
ptr.next = p.next
self.current = ptr
self.no -= 1
def remove_current_node(self) -> None :
self.remove(self.current)
def clear(self) -> None :
while (self.head is not None) :
self.remove_first()
self.current = None
self.no = 0
def next(self) -> bool :
if (self.current is None or self.current.next is None) :
return False
self.current = self.current.next
return True
def print_current_node(self) -> None :
if (self.current is None) :
print("주목 노드 없음")
else :
print(self.current.data)
def print(self) -> None :
ptr = self.head
while (ptr is not None) :
print(ptr.data)
ptr = ptr.next
def __iter__(self) -> LinkedListIterator :
return LinkedListIterator(self.head)
class LinkedListIterator :
def __init__(self, head: Node) :
self.current = head
def __iter__(self) -> LinkedListIterator:
return self
def __next__(self) -> Any :
if (self.current is None) :
raise StopIteration
else :
data = self.current.data
self.current = self.current.next
return data
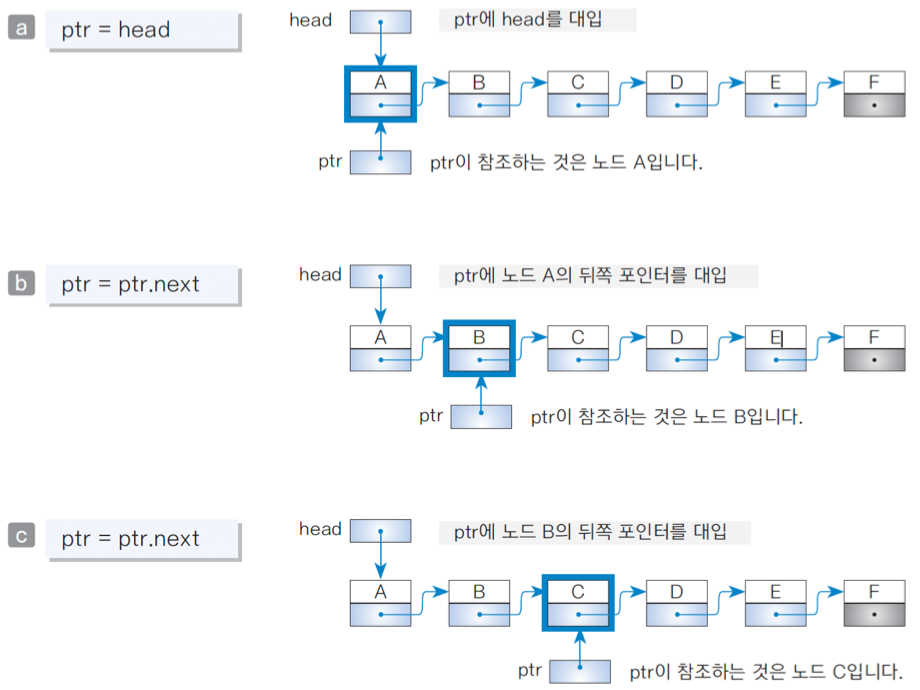
4.7) 노드의 검색 수행 과정
위에서 언급된 search( ) 메서드는 노드의 삭제, 삽입, 탐색 등 다양한 작업에서 사용되는 중요한 메서드이다.
해당 메서드에서 노드를 어떻게 검색하는지, 수행 과정을 살펴보자.
4.8) 머리에 노드 삽입 전/후 비교
add_first( ) 메서드를 사용해 머리에 노드를 삽입할 때, head가 참조하는 주소가 먼저 바뀌면 리스트의 데이터가 유실될 수도 있어 주의가 필요하다.

노드 G를 먼저 노드 A에 연결한 뒤, head가 노드 G를 참조하도록 해야 B~F까지의 노드가 유실되지 않는다.
4.9) 꼬리에 노드 삽입 전/후 비교
add_first( )와 달리, 꼬리에 노드를 삽입하는 add_last( )는 동작 과정이 좀 더 단순하다.
리스트의 맨 끝 위치를 찾기 위해서는 next 필드의 값이 None인 노드를 찾으면 된다.

4.10) 머리 노드 삭제 전/후 비교

4.11) 꼬리 노드 삭제 전/후 비교

4.12) remove( ) 메서드로 노드 삭제 전/후 비교
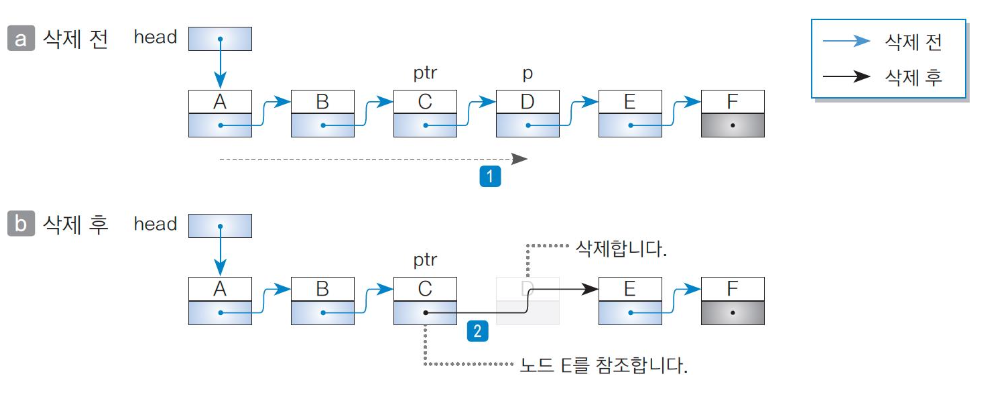
4.13) 포인터를 이용한 연결 리스트의 한계
포인터를 사용한 연결 리스트는 노드 삽입/삭제가 이루어질 때 데이터를 이동할 필요가 없다.
다만, 노드를 삽입/삭제할 때마다 노드용 인스턴스를 생성/소멸되어야 하기 때문에 메모리 자원 소모가 많이 든다.
5. 커서를 이용해 연결 리스트 만들기
프로그램 실행 중, 데이터 개수가 크게 변하지 않거나, 데이터 최대 개수를 예측할 수 있는 조건이라면, 배열을 활용하는 커서를 이용한 연결 리스트 구현 방법이 더 유리하다.
커서(cursor)란, int형 정수값인 인덱스로 나타낸 포인터이다.
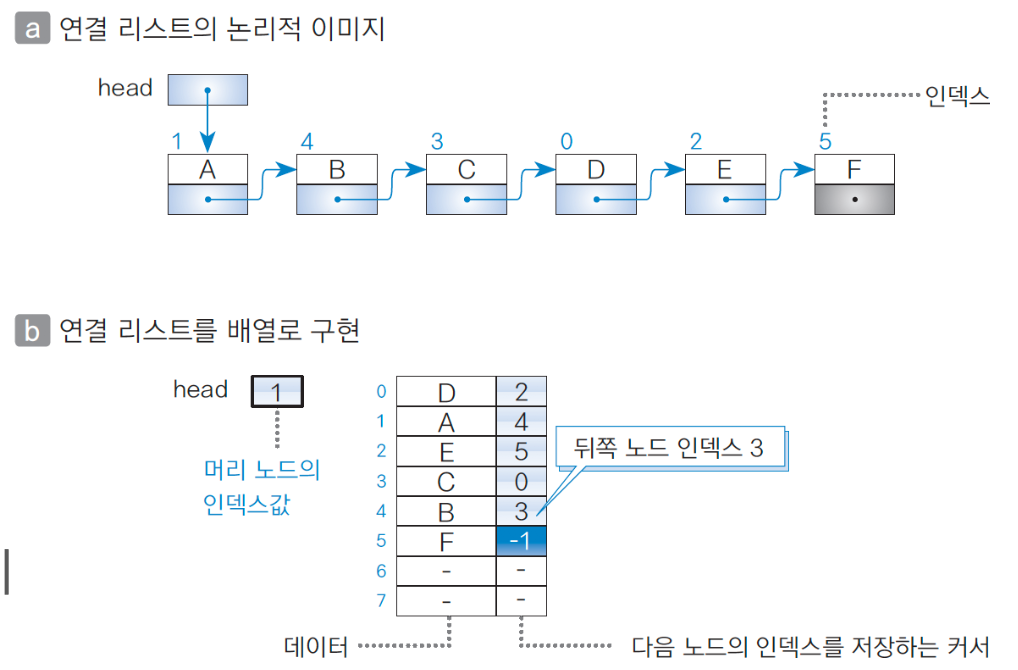
노드 B의 뒤쪽 커서 3은 뒤쪽 노드가 인덱스 3의 위치에 있는 노드 C라는 의미이다.
커서를 이용해 연결 리스트를 구현하면 노드의 삽입과 삭제에 따른 원소 이동이 처음부터 불필요하다.
아래 사진에서 맨 앞의 노드 G를 삽입하는 과정을 살펴보자.
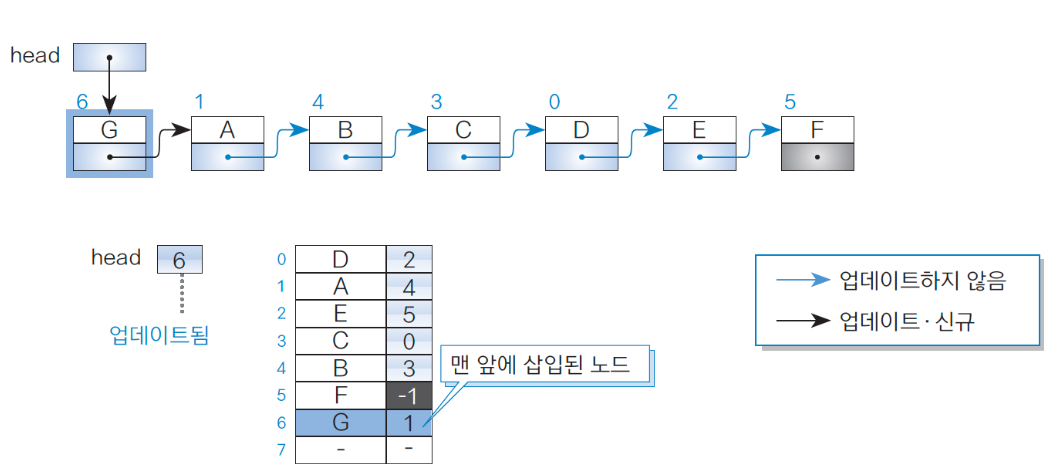
- 배열 안에서 가장 끝 쪽에 있는 인덱스 위치에 저장한다. (이는 연결 리스트 상의 맨 끝을 의미하는 것이 아님)
- head를 1에서 6으로 업데이트하고, 노드 G의 뒤쪽 커서를 1로 설정한다.
5.1) 배열 안에 비어 있는 원소 처리하기
커서를 사용한 연결 리스트 구현 방식은 배열을 사용해 구현한 방식이기 때문에 삭제를 여러 번 반복할 경우, 빈 레코드가 여럿 생기게 된다.
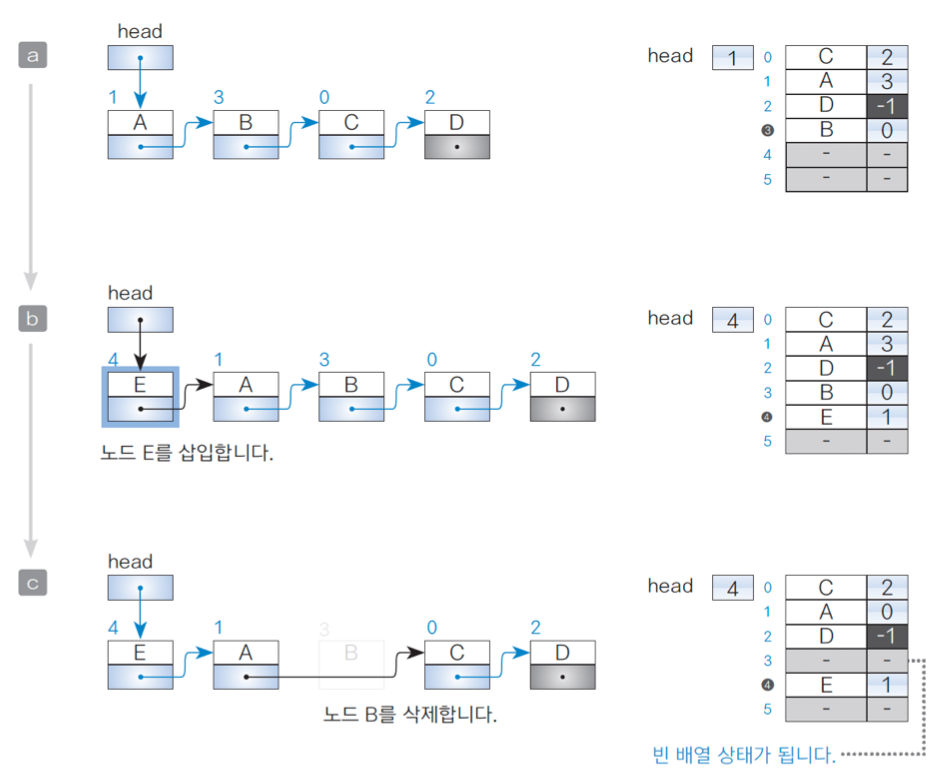
5.2) 프리 리스트 (Free List)
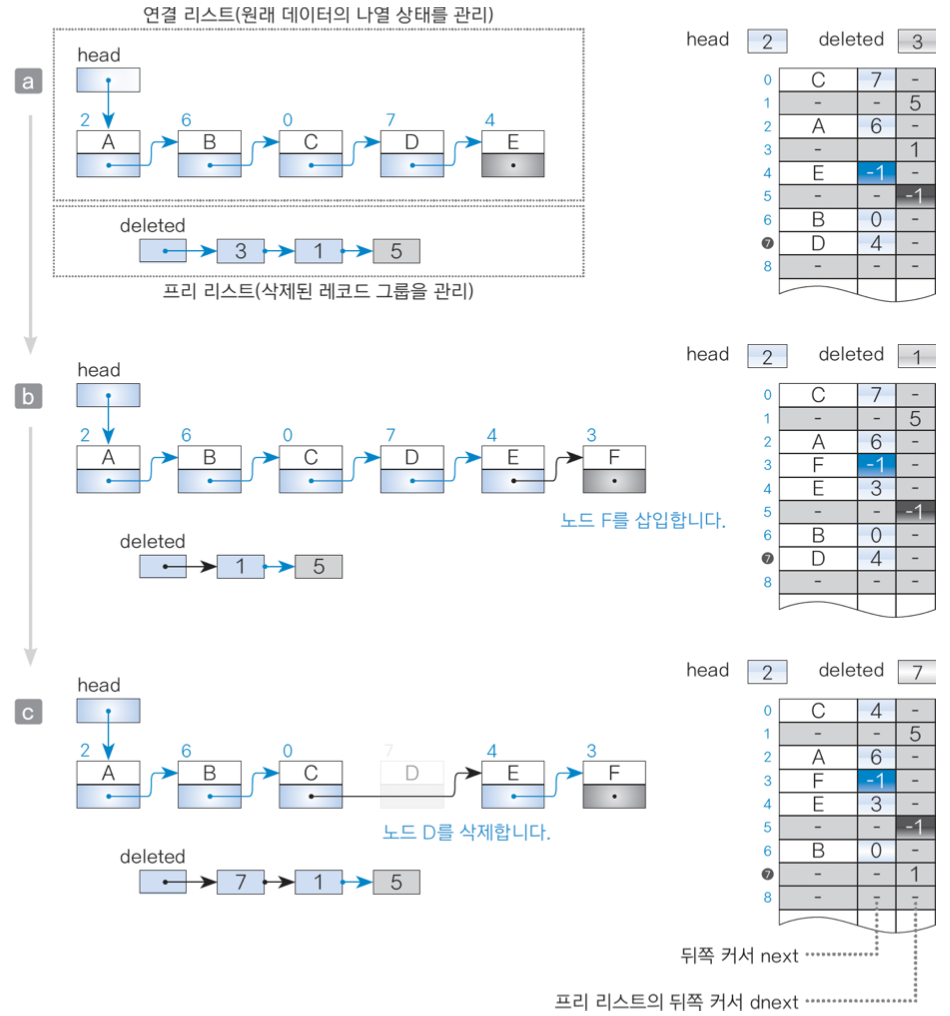
삭제된 레코드 그룹을 관리할 때 사용하는 자료구조이다.
원래 데이터의 순서를 관리하는 연결 리스트와 결합해 구현한다.
- dnext: 프리 리스트 뒤쪽 노드를 참조하는 커서
- deleted: 프리 리스트의 머리 노드를 참조하는 커서
- max: 배열에서 맨 끝 쪽에 저장되는 레코드 번호
연결 리스트에 원소 삽입 시, 프리 리스트가 비어 있지 않으면 프리 리스트 머리 노드에 원소를 저장한다.
프리 리스트가 비어 있다면 배열의 맨 끝의 연결 리스트에서 노드를 삭제한다.
이때, 삭제한 레코드 인덱스를 프리 리스트의 머리 노드로 등록한다.
6. 원형 리스트 (Circular List)

연결 리스트의 꼬리 노드가 다시 머리 노드를 가리키는 원형을 띄고 있는 구조의 리스트이다.
고리 모양으로 늘어서 데이터를 표현하는 데 알맞은 리스트 구조이다.
원형 리스트의 꼬리 노드의 뒤쪽 포인터가 None이 아닌 머리 노드의 포인터 값이 된다.
이 때문에 어떤 노드가 마지막 노드인지를 표기해줄 방법을 마련해야 한다.
7. 이중 연결 리스트 (Double-Linked List)

연결 리스트의 가장 큰 단점인 앞쪽 노드 탐색이 어렵다는 것을 개선하였다.
이중 연결 리스트의 각 노드는 뒤쪽 노드에 대한 포인터, 앞쪽 노드에 대한 포인터가 함께 주어진다.
- data: 데이터 참조
- prev: 앞쪽 노드 참조
- next: 뒤쪽 노드 참조
8. 원형 이중 연결 리스트 (Circular Double-Linked List)

원형 리스트와 이중 연결 리스트를 결합한 구조의 리스트이다.
각 노드는 3개의 필드로 구성된 이중 연결 리스트의 노드와 동일하다.
9. python의 논리 연산자
python에서 사용되는 논리 연산자는 다른 언어와 비교했을 때 조금 난해하다.
다양한 타입의 데이터들을 자유롭게 비교해 불리언(bool) 값을 얻을 수 있는데, 이를 평가하는 기준에서 차이가 난다.
print(5 and 3)
print(5 or 3)
print(0 or 3)
//#RESULT#//
3
5
3이러한 결과가 나온 이유는 다음과 같다.

수고하셨습니다!
'Technology > Algorithm (2022)' 카테고리의 다른 글
| 17. 동적 계획법 (0) | 2022.01.25 |
|---|---|
| 16. 트리 (0) | 2022.01.25 |
| 14. 정렬 알고리즘 (0) | 2022.01.21 |
| 13. 하노이의 탑과 8 Queens (0) | 2022.01.21 |
| 12. 재귀 알고리즘 (0) | 2022.01.19 |




