Develog
5. 배열 본문
1. 배열 원소 최댓값 구하기
배열 a의 원소가 3개인 경우
max = a[0]
if a[1] > max :
max = a[1]
if a[2] > max :
max = a[2]배열 a의 원소가 4개인 경우
max = a[0]
if a[1] > max :
max = a[1]
if a[2] > max :
max = a[2]
if a[3] > max :
max = a[3]코드를 이렇게 작성할 경우, 배열의 크기가 커지면 if문의 개수도 많아지기 때문에 적합하지 않다.
2. 배열 원소의 최댓값 구하기
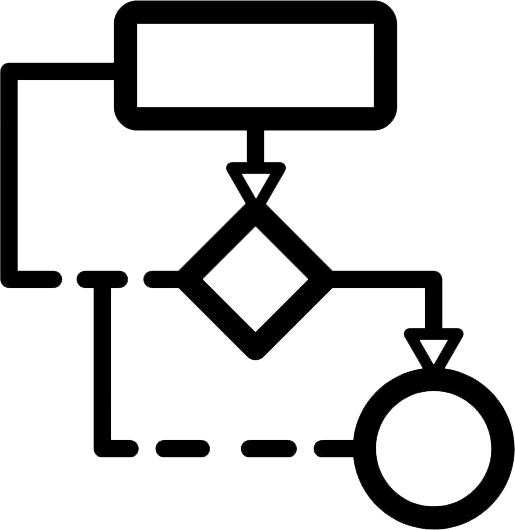
배열 원소의 최댓값을 구하는 과정은 다음과 같다.
- 원소(a[0])의 값을 maximum에 대입한다.
- 필요에 따라 if 문에서 maximum 값을 업데이트한다.
- 원소 수가 n일 경우, if문은 n-1번 실행된다.
이 과정을 순서도로 표현하면 다음과 같다.
스캔(scan)이란, 배열 원소를 1개씩 차례로 주목하며 살펴보는 방식을 나타내는 알고리즘 용어이다.
트래버스(traverse) 또는 주사라고도 한다.
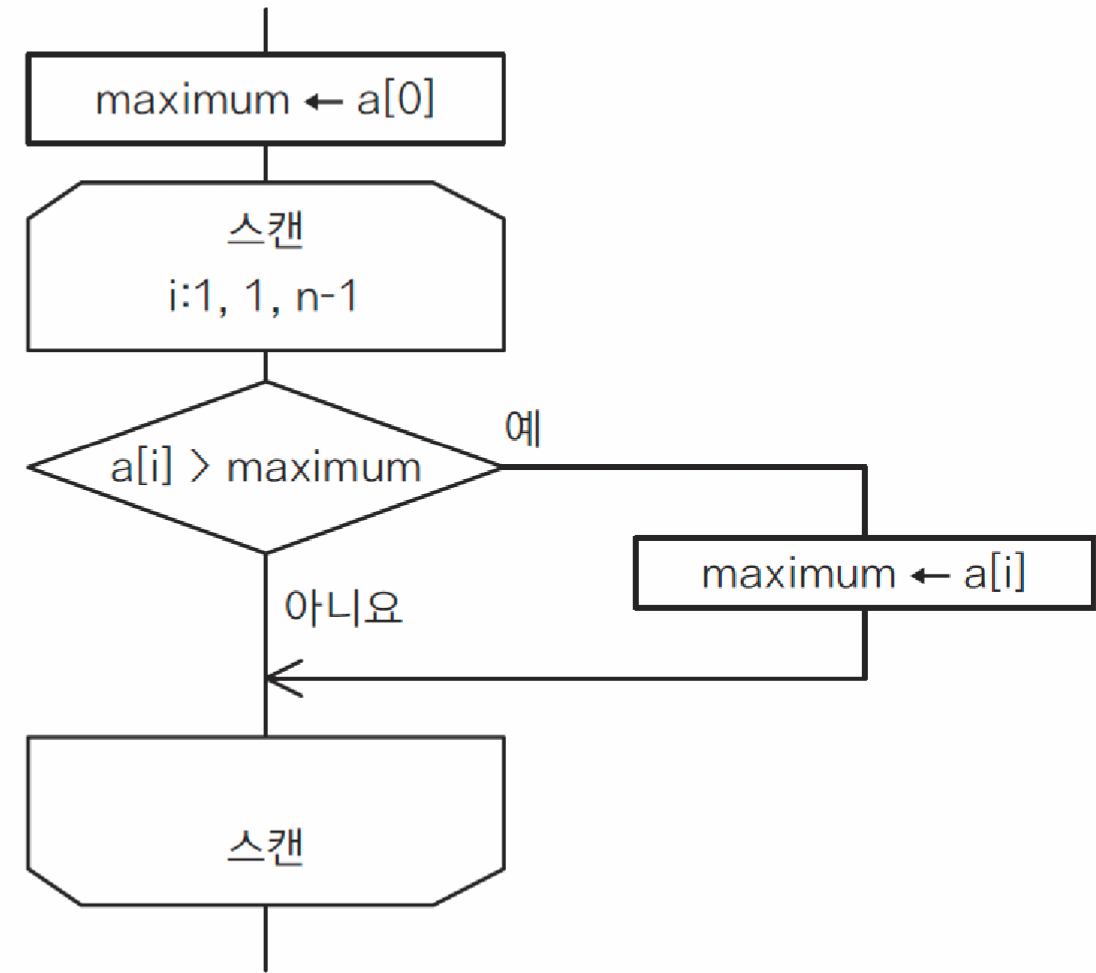
2.1) 배열 원소의 최댓값을 구하는 함수
def max_of(a) :
max = a[0]
for i in range(1, len(a)) :
if (a[i] > max) :
max = a[i]위 코드의 동작 과정은 다음과 같다.
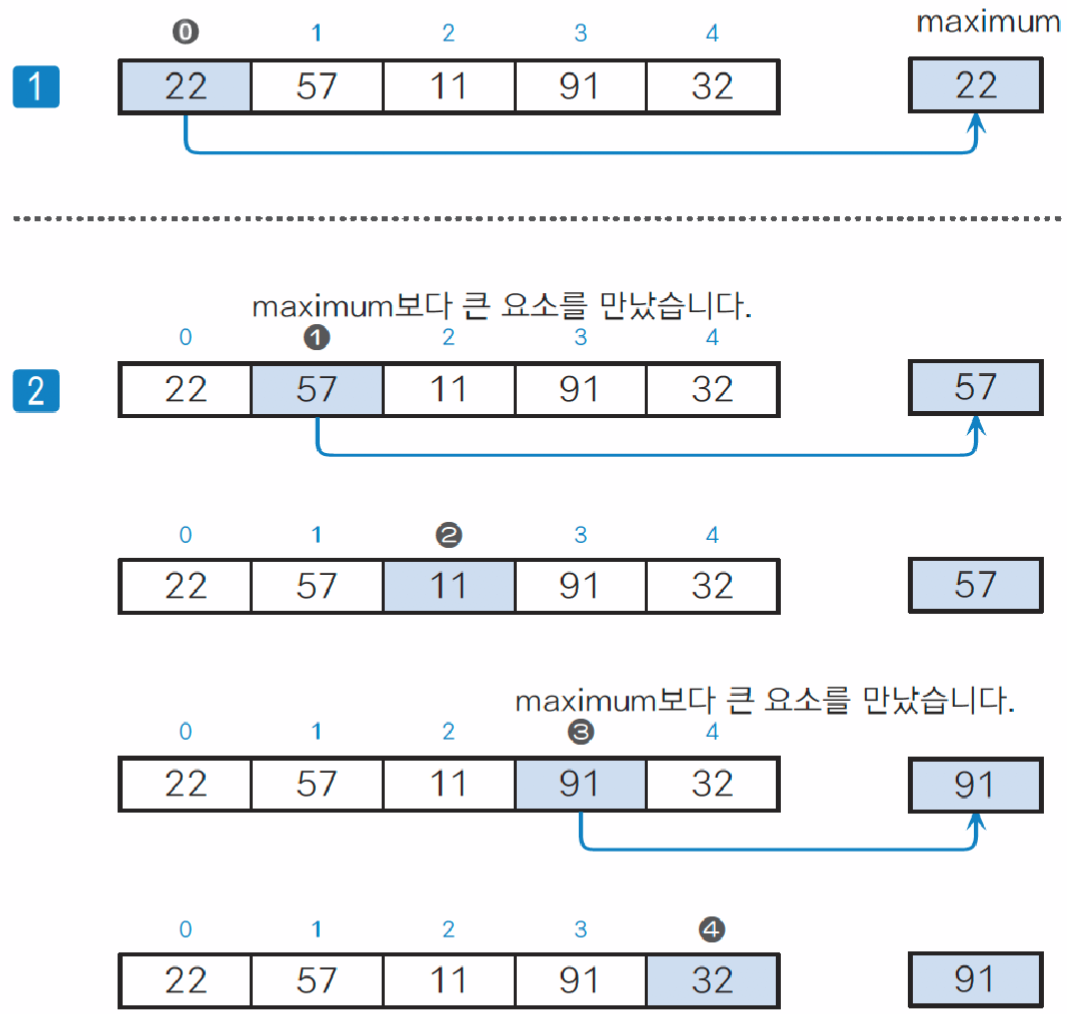
2.2) 배열 원소의 최댓값을 구하는 알고리즘
이제 위에서 언급한 max_of() 함수를 사용해 전체 코드를 작성해보자.
from typing import Any, Sequence
def max_of(a: Sequence) -> Any :
max = a[0]
for i in range(1, len(a)) :
if (a[i] > max) :
max = a[i]
return max
if (__name__ == '__main__') :
print('배열의 최댓값을 구합니다.')
num = int(input("원소 수를 입력하세요: "))
x = [None] * num
for i in range(num) :
x[i] = int(input(f"x[{i}] 값을 입력하세요: "))
print(f"최댓값: {max_of(x)}")max_of( ) 함수는 배열 a의 최댓값을 반환한다.
2.3) 타입 어노테이션/타입 힌트 (Type Annotation / Type Hint)
위에 나온 전체 코드를 살펴보면, max_of( ) 함수의 매개변수 옆에 Sequence 키워드가 붙은 것을 알 수 있다.
이는 매개 변수의 타입을 알려주는 키워드이다.
python에서는 변수의 타입을 고정해서 선언하지 않기 때문에, 개발자가 해당 변수의 타입이 어떤 타입인지를 쉽게 파악할 수 있도록 도와주는 역할을 한다.
위 코드를 예시로 들면 다음과 같다.
매개 변수 a의 자료형은 Sequence 형이며, 반환하는 타입은 Any 형이다.
- Any: 제약이 없는 임의의 자료형
- Sequence: 리스트, 튜플, 문자열 등 순서가 있는 시퀀스 자료형
2.4) max_of() 함수의 특징
함수 안에서는 배열 a의 원소를 변경하지 않는다.
호출하는 쪽이 넘겨주는 실제 인수의 자료형은 뮤터블(mutable)인 리스트(list), 이뮤터블(imutable)인 튜플(tuple), 문자열(string) 등 시퀀스 자료형이라면 무엇이든 상관없다.
인수의 원소를 비교 연산자 >로 값을 비교할 수 있다면, 다른 형(int 형, float 형)이 섞여도 된다.
최댓값의 원소가 int 형 원소라면, int 형 원소를, float 형 원소면 float 형 원소를 반환한다.
3. 재사용할 수 있는 모듈 작성
모듈(module)이란, 1개의 파이썬(python) 스크립트 프로그램이다.
확장자(.py)를 제외한 파일 이름 자체를 모듈 이름으로 사용한다.
아래 예시 코드를 먼저 보자.
if (__name__ == '__main__') :여기서 __name__이 모듈 이름 변수이다.
스크립트 프로그램이 직접 실행될 때, '__name__' 모듈 이름 변수의 값이 '__main__'으로 고정된다.
만약 다른 스크립트에 임포트(import)되는 경우에는 기존 모듈 이름을 사용한다.
모듈은 프로그램이 처음 임포트 되는 시점에서 모듈 객체가 생성되며 초기화되는 구조이다.
즉, 위의 if 문 예시는 해당 파이썬 스크립트 프로그램이 직접 실행되었을 때 참(true)이 나오는 조건문이다.
다른 언어에 비유하자면 main() 함수에 해당한다.
모듈은 서로 같은 디렉터리(폴더) 안에 있어야 한다.
3.1) 모듈 테스트
정수를 사용자에게 차례대로 입력받다가 End를 입력하면 종료, 입력된 배열의 크기와 배열 원소의 최댓값을 출력하는 알고리즘을 작성해보자.
모듈 max의 max_of() 함수를 임포트 해서 구현한다.
from max import max_of
print("배열의 최댓값을 구합니다.")
print("End를 입력하면 종료합니다.")
num = 0
x = []
while (True) :
s = input(f"x[{num}] 값을 입력하세요.: ")
if (s == 'End') :
break
x.append(int(s))
num += 1
print(f"{num}개 입력됨.")
print(f"최댓값: {max_of(x)}")
3.2) random 모듈을 이용해 배열의 원소를 난수로 결정하는 알고리즘
배열의 원소 수, 최댓값, 최솟값을 사용자에게 입력받고, random 모듈을 이용해 난수로 배열을 구성해 출력하는 알고리즘을 작성해보자.
import random
from max import max_of
print("난수로 배열을 구성해 출력하는 알고리즘")
num = int(input("난수의 개수: "))
lo = int(input("난수의 최솟값: "))
hi = int(input("난수의 최댓값: "))
x = [None] * num
for i in range(num) :
x[i] = random.randnt(lo, hi)
print(f'{(x)}')
print(f"최댓값: {max_of(x)}")
3.3) 각 배열 원소의 최댓값을 구해서 출력하는 알고리즘
튜플, 문자열, 문자열 리스트의 최댓값을 구하는 알고리즘을 작성해보자.
from max import max_of
t = (4, 7, 5.6, 2, 3.14, 1)
s = "string"
a = ["dts", "aac", "flac"]
print(f"{t}의 최댓값 {max_of(t)}")
print(f"{s}의 최댓값 {max_of(s)}")
print(f"{a}의 최댓값 {max_of(a)}")
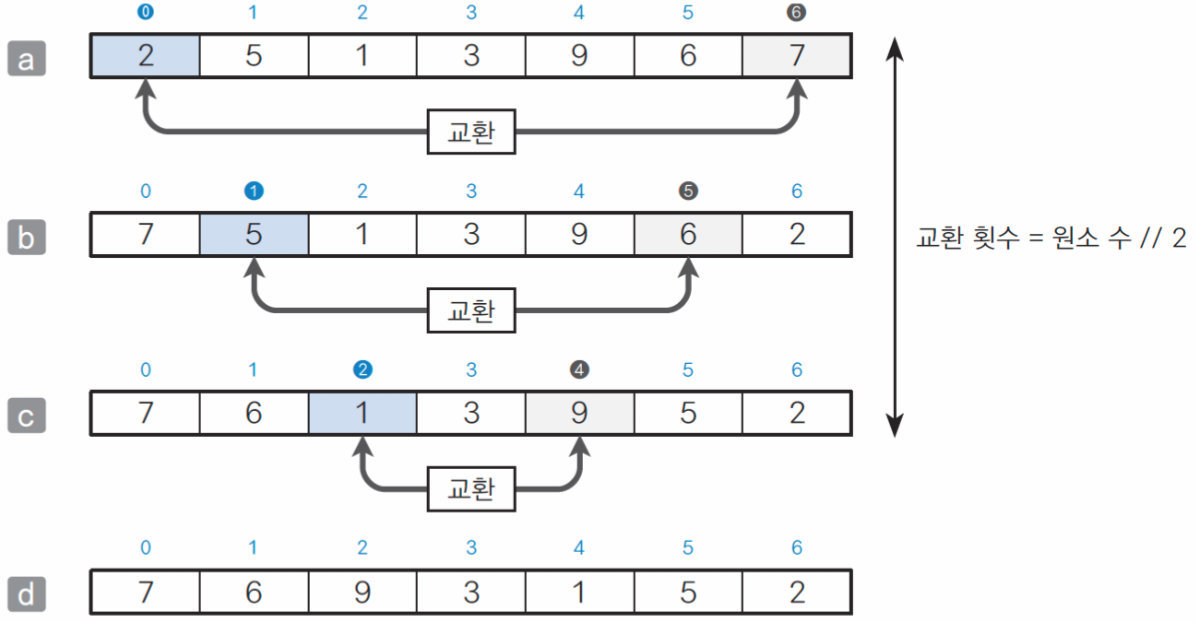
4. 배열 원소를 역순으로 정렬하는 알고리즘
맨 앞 원소 a[0], 맨 끝 원소 a[6]의 값을 교환한다.
1개씩 안쪽의 원소를 교환하는 작업을 반복한다.
원소 수가 홀수인 경우, 가운데 원소는 교환할 필요가 없다.
총 교환 횟수는 (원소 수) // 2번이다.
from typing import Any, MutableSequence
def reverse_array(a: MutableSequence) -> None :
n = len(a)
for i in range(n // 2) :
a[i], a[n-i-1] = a[n-i-1], a[i]
if (__name__ == "__main__") :
print("배열 원소 역순 정렬")
nx = int(input("원소 수: "))
x = [None] * nx
for i in range(nx) :
x[i] = int(input(f"x[{i}] 값: "))
reverse_array(x)
for i in range(x) :
print(f"x[{i}] = {x[i]}")
4.1) 표준 라이브러리를 사용해 역순으로 정렬하기
python에서 제공하는 표준 라이브러리를 사용해 역순 정렬을 구현해보자.
list형의 reverse() 함수는 자기 자신을 역순으로 정렬한다.
reversed() 함수는 원소를 역순으로 꺼내는 이터레이터를 반환한다.
이를 활용하여 list() 함수의 인자로 reversed() 함수의 반환 객체를 사용하면, 역순으로 정렬한 리스트를 생성할 수 있다.
x.reverse()
y = list(reversed(x))
5. 기수 변환
기수란, 수를 나타내는데 기초가 되는 수이다.
10진수의 기수: 0 1 2 3 4 5 6 7 8 9
10진수의 각 자리는 10의 거듭제곱 값을 가진다.
1234 == (1 * 10^3) + (2 * 10^2) + (3 * 10^1) + (4 * 10^0)
5.1) 기수 변환 알고리즘
정수를 임의의 기수로 변환하는 알고리즘을 구현해보자.
정수를 n으로 나눈 나머지를 구하는 동시에, 몫을 반복해서 나눠줘야 한다.
몫이 0이 될 때까지 이 과정을 반복한 후, 나머지를 역순으로 늘어놓아 기수로 변환한 수를 얻는다.
from typing import Any
def card_conv(x: int, r:int) -> str :
d = ""
dchar = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"
n = len(str(x))
print(f"{r:2} || {x:{n}d}")
while (x > 0) :
d += dchar[x % r]
x //= r
return d[::-1]
if (__name__ == "__main__") :
print("10진수를 n진수로 변환")
while (True) :
while (True) :
no = int(input("변환할 값으로 음이 아닌 정수 입력: "))
if (no > 0) :
break
while (True) :
cd = int(input("변환할 진수 입력: "))
if (2 <= cd <= 36) :
break
print(f"{cd}진수로는 {card_conv(no, cd)}")
re = input("한 번 더 변환할까요? (Y/n)")
if (re in {"n", "N"}) :
break
6. 소수 열하기
6.1) 1000 이하의 모든 소수 찾기 알고리즘
counter = 0
for n in range(2, 1001) :
for i in range(2, n) :
counter += 1
if (n % i == 0) :
break
else :
print(n)
print(f"나눗셈 횟수: {counter}")n이 소수일 때, for 문이 중단되지 않고 끝까지 수행되려면, else 문을 실행해 n 값을 출력한다.
n이 합성수일 때, for 문을 중단한다.
실행되는 모든 경우의 수를 따져보면 다음과 같다.
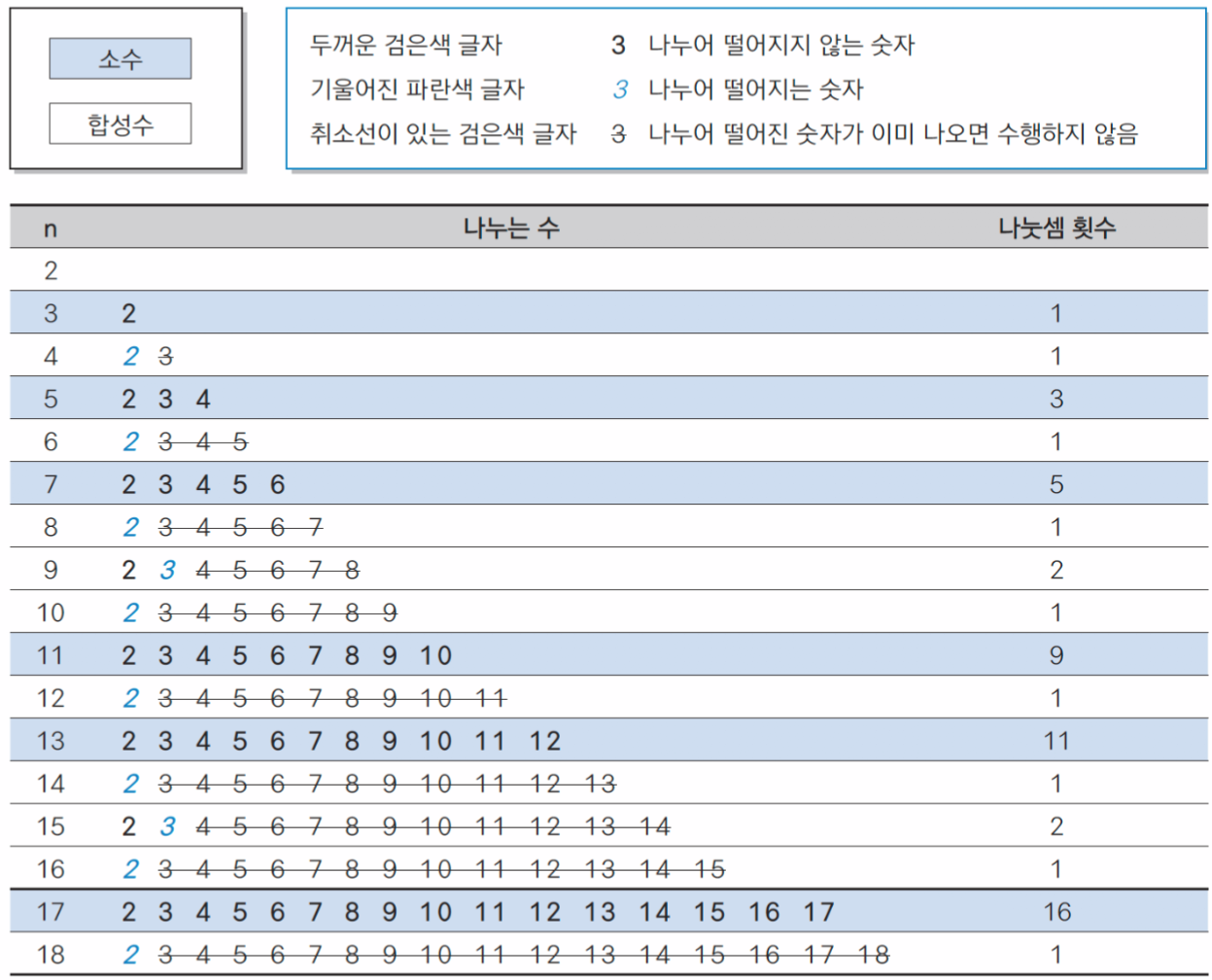
사진을 보면 알 수 있듯이, 필요 이상으로 연산이 이루어지고 있다.
이제 최적화를 시작해보자.
6.2) 1000 이하의 모든 소수를 나열하는 알고리즘 개선 1
소수를 구하는 과정에서 지금까지 구한 소수를 배열의 원소로 저장한다.
다음 수를 판단할 때, 배열에 저장된 소수로 나눗셈을 진행한다.
4 이상의 짝수는 2로 나눠도 떨어지므로, 판단을 생략하고, 3부터 시작해서 2씩 증가시킨다.
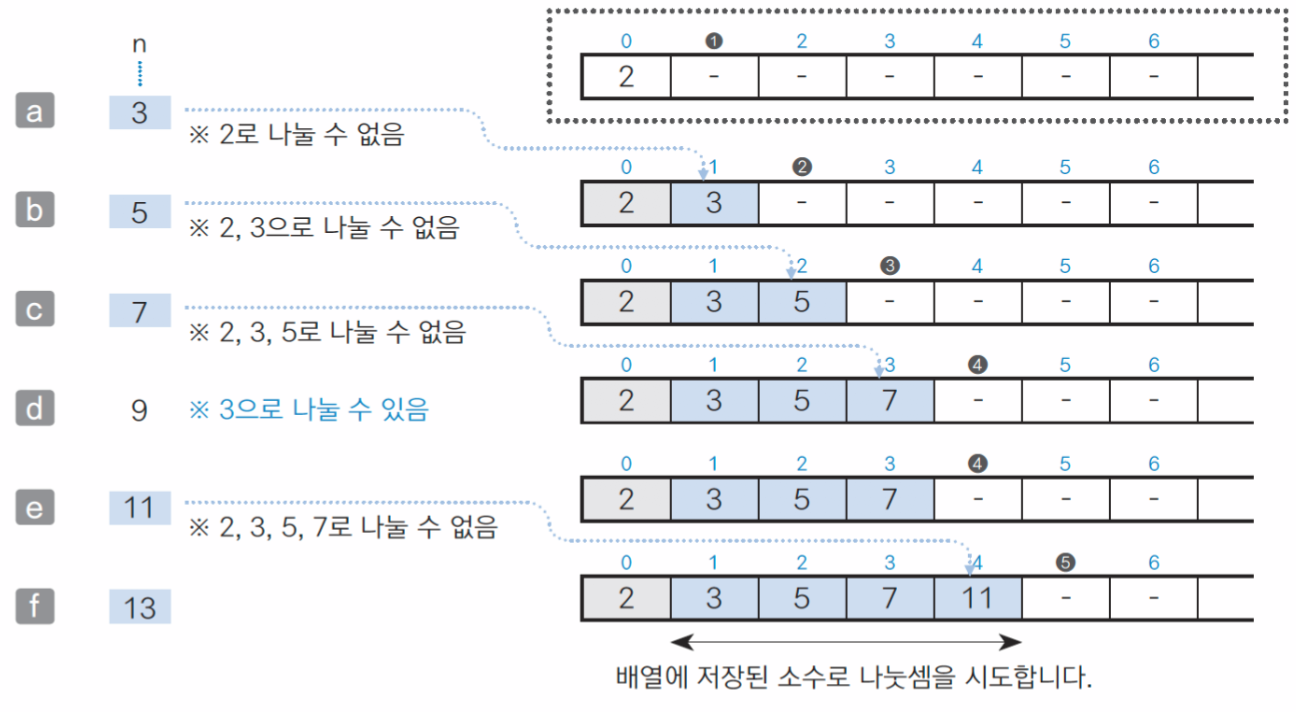
소수를 구하는 과정에서 지금까지 구한 소수를 배열 prime에 저장한다.
n이 소수인지 판단할 때, 배열 prime에 저장한 소수로 나눗셈을 진행한다.
이렇게 코드를 작성하면 속도는 개선되지만, 메모리가 희생된다.
counter = 0
ptr = 0
prime = [None] * 500
prime[ptr] = 2
ptr += 1
for n in range(3, 1001, 2) :
for i in range(1, ptr) :
counter += 1
if (n % prime[i] == 0) :
break
else :
prime[ptr] = n
ptr += 1
for i in range(ptr) :
print(prime[i])
print(f"나눗셈 횟수: {counter}")
6.3) 1000 이하의 모든 소수를 나열하는 알고리즘 개선 2
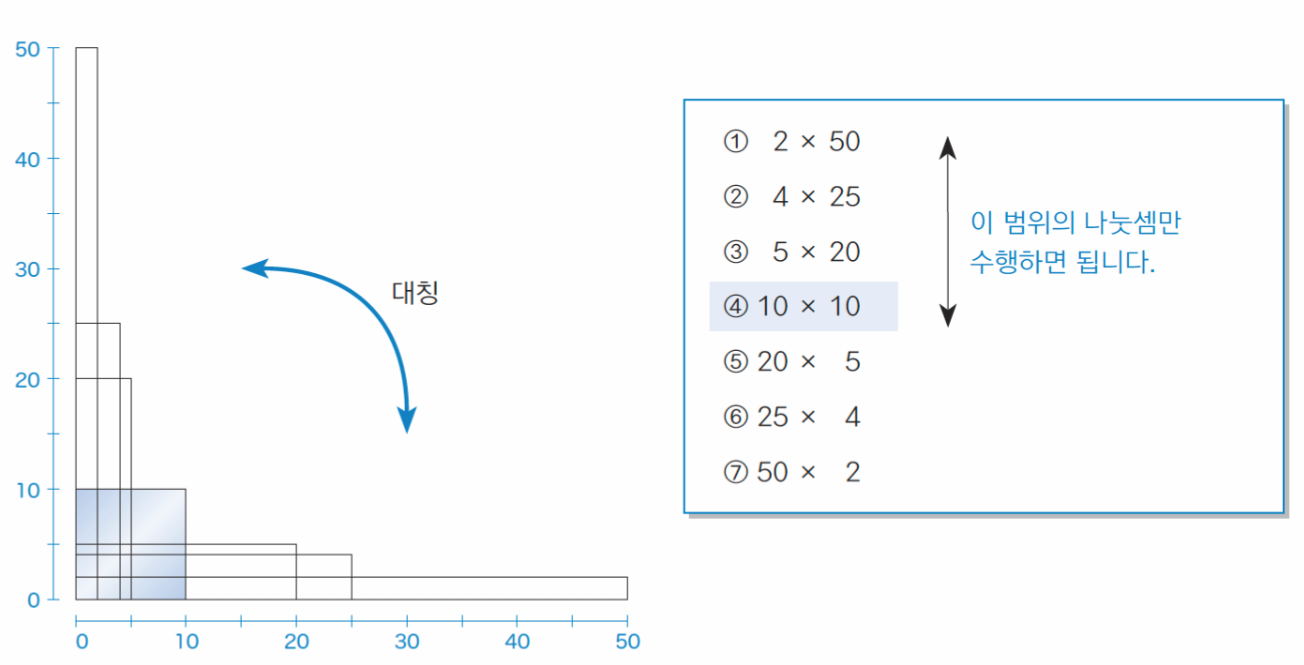
넓이가 100인 직사각형이 있다고 가정한다.
가로, 세로 변의 길이가 5*20인 직사각형과 20*5인 직사각형은 서로 같은 직사각형이다.
모든 직사각형은 정사각형 10*10을 경계로 대칭을 이룬다.
만약 100이 5로 나눠 떨어진다면, 20으로도 나눠 떨어진다.
정사각형 한 변의 길이만 나눗셈을 시도하고, 그 과정에서 1번이라도 나눠 떨어지면 소수가 아니라고 판단한다.
이를 정리하면, n의 제곱근 이하의 어떤 소수로도 나눠 떨어지지 않는 자연수 n은 소수이다.
counter = 0
ptr = 0
prime = [None] * 500
prime[ptr] = 2
ptr += 1
prime[ptr] = 3
ptr += 1
for n in range(5, 1001, 2) :
i = 1
while (prime[i] * prime[i] <= n) :
counter += 2
if (n % prime[i] == 0) :
break
i += 1
else:
prime[ptr] = n
ptr += 1
counter += 1
for i in range(ptr) :
print(prime[i])
print(f"곱셈, 나눗셈 실행 횟수: {counter}")prime[i] * prime[i]이 n보다 작은지 판단한다. == prime[i]가 n의 제곱근보다 작은지 판단한다.
(이는 제곱근 연산이 곱셈보다 느리기 때문에 사용하는 편법이다)
나눗셈 비용 외에 곱셈 비용이 추가로 소모된다.
나눗셈과 곱셈은 소모되는 비용이 동일하다.
수고하셨습니다!
'Technology > Algorithm (2022)' 카테고리의 다른 글
| 7. 선형 검색 (0) | 2022.01.11 |
|---|---|
| 6. 리스트와 튜플 (0) | 2022.01.11 |
| 4. Python 변수 (0) | 2022.01.04 |
| 3. 자료구조와 배열 (0) | 2022.01.03 |
| 2. 반복 알고리즘 (0) | 2021.12.30 |





